Phương pháp giải:

Thể tích khối chóp \(V=\frac{1}{3}S.h\) với \(S\) là diện tích đáy, \(h\) là chiều cao.

Lời giải chi tiết:

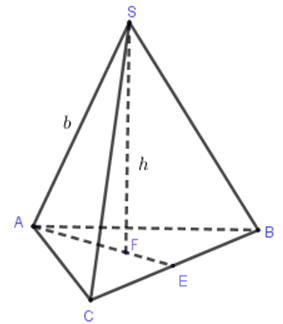
Gọi F là tâm đường tròn ngoại tiếp tam giác ABC \(\Rightarrow SF\bot \left( ABC \right)\)

Xét hình chóp tam giác đều như hình bên.

Xét \(\Delta SAF\) vuông tại \(F\) có \(AF=\sqrt{S{{A}^{2}}-S{{F}^{2}}}=\sqrt{{{b}^{2}}-{{h}^{2}}}\Rightarrow AE=\frac{3}{2}AF=\frac{3}{2}\sqrt{{{b}^{2}}-{{h}^{2}}}\).

Tam giác \(ABC\) đều có chiều cao \(AE=\frac{BC\sqrt{3}}{2}=\frac{3}{2}\sqrt{{{b}^{2}}-{{h}^{2}}}\Rightarrow BC=\sqrt{3}.\sqrt{{{b}^{2}}-{{h}^{2}}}\)

Do đó

\(\begin{align} & {{V}_{S.ABC}}=\frac{1}{3}{{S}_{ABC}}.SF=\frac{1}{3}.\frac{1}{2}AE.BC.SF \\  & =\frac{1}{3}.\frac{1}{2}.\frac{3}{2}\sqrt{{{b}^{2}}-{{h}^{2}}}.\sqrt{3}\sqrt{{{b}^{2}}-{{h}^{2}}}.h=\frac{\sqrt{3}}{4}\left( {{b}^{2}}-{{h}^{2}} \right)h \\ & \Rightarrow {{V}_{S.ABC}}=\frac{\sqrt{3}}{4}\left( {{b}^{2}}-{{h}^{2}} \right)h \\ \end{align}\)

Chọn A.