Câu hỏi
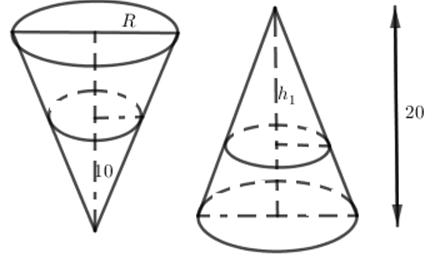
Một cái phễu có dạng hình nón, chiều cao của phễu là \(20cm\). Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu là \(10cm\). Nếu bịt kín miệng phễu rồi lật ngược lên thì chiều cao cột nước trong phễu bằng giá trị nào sau đây?
- A \(1,07cm\)
- B \(2,87cm\)
- C \(0,87cm\)
- D \(3,87cm\)
Phương pháp giải:
Cho khối nón \(\left( S \right)\) có thể tích \(V\), chiều cao \(h\) bị cắt bởi mặt phẳng vuông góc với trục, chia khối nón thành hai phần: Khối nón \({{S}_{1}}\) có thể tích \({{V}_{1}}\), chiều cao \({{h}_{1}}\) và một khối nón cụt. Khi đó \(\frac{{{V}_{1}}}{V}={{\left( \frac{{{h}_{1}}}{h} \right)}^{3}}\).
Lời giải chi tiết:
Gọi \(V'\) là thể tích cột nước có chiều cao \(10cm\), \(V\) là thể tích khối nón, \({{V}_{1}}\) là thể tích khối nón nhỏ phía trên (phần không có nước) sau khi bị úp ngược.
Khi đó
\(\begin{align} & V'=\frac{1}{3}\pi R_{1}^{2}.10;V=\frac{1}{3}\pi {{R}^{2}}.20 \\ & \Rightarrow \frac{V'}{V}={{\left( \frac{10}{20} \right)}^{3}}=\frac{1}{8}\Rightarrow \frac{{{V}_{1}}}{V}=\frac{7}{8} \\ & \Rightarrow {{\left( \frac{{{h}_{1}}}{h} \right)}^{3}}=\frac{7}{8}\Rightarrow {{h}_{1}}=\sqrt[3]{\frac{7}{8}{{.20}^{3}}}=19,13 \\ & \Rightarrow {{h}_{2}}=20-19,13=0,87cm \\ \end{align}\)
Chọn C.