Câu hỏi
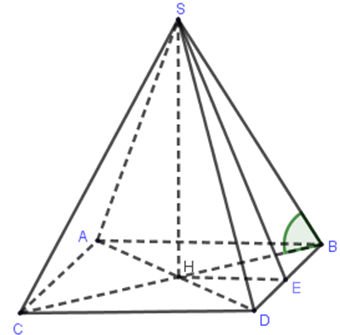
Cho hình chóp đều \(S.ABCD\) đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên hợp với đáy một góc \({{45}^{0}}\). Hình nón tròn xoay đỉnh \(S\), đáy là đường tròn nội tiếp hình vuông \(ABCD\), có diện tích xung quanh là:
- A \(\frac{\pi {{a}^{2}}}{2}\)
- B \(\frac{5\pi {{a}^{2}}}{2}\)
- C \(\frac{3\pi {{a}^{2}}}{2}\,\)
- D \(\frac{{\pi {a^2}\sqrt 3 }}{4}\)
Phương pháp giải:
- Xác định góc giữa cạnh bên và mặt đáy dựa vào định nghĩa: “Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng”.
- Tính bán kính hình tròn nội tiếp đa giác đáy và độ dài đường sinh.
- Diện tích xung quanh hình nón được tính bởi công thức \({{S}_{xq}}=\pi rl\).
Lời giải chi tiết:
Hình chóp \(S.ABCD\) đều nên \(SH\) là đường cao (\(H\) là giao điểm hai đường chéo của hình vuông \(ABCD\))
Do đó \(\left( \widehat{SB,\left( ABCD \right)} \right)=\widehat{SBH}={{45}^{0}}\Rightarrow SH=HB=\frac{a\sqrt{2}}{2}\)
Đường tròn đáy của hình nón chính là đường tròn nội tiếp hình vuông \(ABCD\) có bán kính \(r=HE=\frac{a}{2}\).
Độ dài đường sinh \(l=SE=\sqrt{S{{H}^{2}}+H{{E}^{2}}}=\sqrt{{{\left( \frac{a\sqrt{2}}{2} \right)}^{2}}+{{\left( \frac{a}{2} \right)}^{2}}}=\frac{a\sqrt{3}}{2}\).
Vậy diện tích xung quanh \({{S}_{xq}}=\pi rl=\pi .\frac{a}{2}.\frac{a\sqrt{3}}{2}=\frac{\pi {{a}^{2}}\sqrt{3}}{4}\)
Chọn D