Phương pháp giải:

Sử dụng tính chất cạnh huyền lớn hơn cạnh góc vuông.

Lời giải chi tiết:

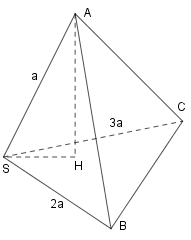
Gọi \(AH\) là đường cao của hình chóp \({\rm{AS}}BC\) khi đó theo công thức thể tích hình chóp ta có \({V_{ASBC}} = \dfrac{1}{3}AH.{S_{SBC}} \le \dfrac{1}{3}AS.{S_{SBC}} = \dfrac{1}{3}a.\left( {\dfrac{1}{2}SB.SC.\sin \widehat {BSC}} \right) \le \dfrac{1}{6}a.\left( {2a} \right)\left( {3a} \right) = {a^3}.\)

Đẳng thức xảy ra khi và chỉ khi \(AS = AH,\,\,\sin \widehat {BSC} = 1 \Leftrightarrow AS = AH,\,SB \bot SC.\) Hay \(SA\) vuông góc với mặt \(\left( {SBC} \right)\) và \(\Delta SBC\) là tam giác vuông tại \(S.\) Và do đó \(SA,\,SB,\,SC\) đôi một vuông góc với nhau.

Chọn C.