Phương pháp giải:

Chứng minh \(\dfrac{{{S_{A'B'C'}}}}{{{S_{ABC}}}} = \dfrac{1}{4}\) và sử dụng \(d\left( {S,A'B'C'} \right) = d\left( {S,ABC} \right)\) để suy ra \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{1}{4}.\)

Lời giải chi tiết:

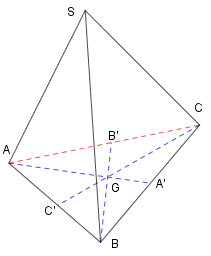
Vì ảnh của \(A,B,C\) qua trọng tâm \(G\) ứng với \(k =  - \dfrac{1}{2}\) nên \(A',\,B',\,C'\) lần lượt là trung điểm của \(BC,\,AC,\,AB.\) Do đó

\(\dfrac{{{S_{A'B'C'}}}}{{{S_{ABC}}}} = \dfrac{{d\left( {A',\,B'C'} \right)B'C'}}{{d\left( {A,BC} \right)BC}} = \dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4}.\)

Do \(\left( {A'B'C'} \right) \equiv \left( {ABC} \right)\) nên \(d\left( {S,A'B'C'} \right) = d\left( {S,ABC} \right).\)

Vì vậy \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{{S_{A'B'C'}}}}{{{S_{ABC}}}} = \dfrac{1}{4}.\)

Chọn A.