Câu hỏi
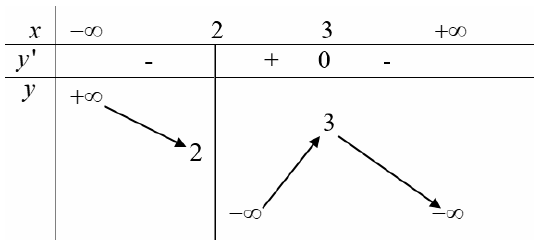
Cho hàm số \(y = f\left( x \right)\) xác định trên \(R\backslash \left\{ 2 \right\},\) liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau. Tìm tập hợp tất cả các giá trị của tham số thực \(m\) sao cho phương trình \(f\left( x \right) = m\) có ba nghiệm phân biệt.
- A \(m \in \left[ {2;3} \right).\)
- B \(m \in \left( {2;3} \right].\)
- C \(m \in \left[ {2;3} \right].\)
- D \(m \in \left( {2;3} \right).\)
Phương pháp giải:
Để phương trình \(f\left( x \right) = m\) có ba nghiệm phân biệt thì đường thẳng y = m cắt đồ thị hàm số y = f(x) tại 3 điểm phân biệt.
Lời giải chi tiết:
Tập hợp các giá trị của tham số thực \(m\) để phương trình \(f\left( x \right) = m\) có ba nghiệm phân biệt là \(m \in \left( {2;3} \right).\)
Chọn D.
Câu hỏi trước
