Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Tìm tất cả những giá trị thực của m để phương trình \(\left| {f\left( x \right)} \right| = m\) có bốn nghiệm phân biệt
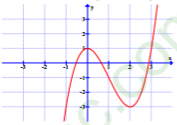
- A \(m \in \left( {1;3} \right)\)
- B \(m \in \left( {1; + \infty } \right)\)
- C \(m \in \left( {0;3} \right)\)
- D \(m \in \left( {\dfrac{1}{2};\dfrac{3}{2}} \right)\)
Phương pháp giải:
Bước 1: Dựa vào đồ thị hàm số \(y = f\left( x \right)\) suy ra đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\)
Bước 2: Áp dụng lý thuyết tương giao giữa hai đồ thị
Lời giải chi tiết:
Ta có:
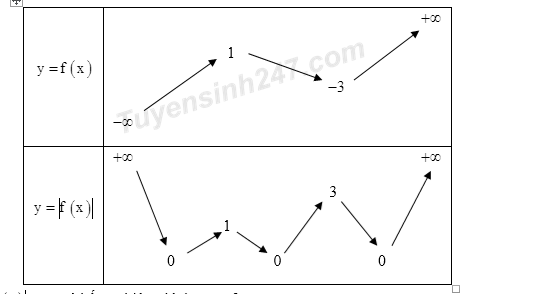
Để phương trình \(\left| {f\left( x \right)} \right| = m\) có bốn nghiệm thì \(1 < m < 3\)
Chọn A.
Câu hỏi trước
