Câu hỏi
Hàm số nào sau đây có đồ thị như hình vẽ?
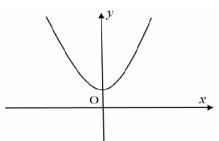
- A \(y = {x^4} + 2{x^2} + 1.\)
- B \(y = {x^4} - 2{x^2} + 1.\)
- C \(y = - {x^4} - 2{x^2} + 1.\)
- D \(y = {x^3} + 3x + 1.\)
Phương pháp giải:
Quan sát đồ thị để đưa ra tính chất và sau đó loại các phương án sai.
Lời giải chi tiết:
Quan sát đồ thị hàm số ta thấy \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty \) do đó ta loại đáp án \(C,\,D\) vì \(\mathop {\lim }\limits_{x \to - \infty } \left( { - {x^4} - 2{x^2} + 1} \right) = - \infty ,\,\,\mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} + 3x + 1} \right) = - \infty .\)
Hàm số có điểm cực tiểu là \(A\left( {0;a} \right),\,\,a > 0.\) Do đó ta loại đáp án B vì hàm số \(y = {x^4} - 2{x^2} + 1\) có điểm cực tiểu là \(\left( {1;0} \right)\) hoặc \(\left( { - 1;0} \right).\)
Đáp án A thỏa mãn.
Chọn A.







