Môn Toán - Lớp 12
Môn Toán - Lớp 12
 30 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ nhận biết
30 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ nhận biết
Câu hỏi
Giá trị lớn nhất của hàm số \(y=\sqrt{5-{{x}^{2}}}+x\) là:
- A \(\pi \).
- B \( \frac{\sqrt{41}}{2}\).
- C \(\sqrt{10}\).
- D \(\frac{\sqrt{89}}{3}\).
Phương pháp giải:
Tìm tập xác định của hàm số, sử dụng MTCT tìm GTLN của hàm số.
Lời giải chi tiết:
TXĐ : \(D=\left[ -\sqrt{5};\sqrt{5} \right]\)
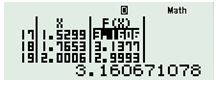
Sử dụng MTCT, ấn [MODE] [7], nhập hàm số \(y=\sqrt{5-{{x}^{2}}}+x\), \( Start=-\sqrt{5}\), \(End=\sqrt{5}\), \(Step=\frac{\sqrt{5}-\left( -\sqrt{5} \right)}{19}\) ta được :
\(\Rightarrow \underset{\left[ -\sqrt{5};\sqrt{5} \right]}{\mathop{\max }}\,y\approx 3,16\approx \sqrt{10}\)
Chọn C.