Câu hỏi
Cho tam giác đều ABC có cạnh bằng 100. Người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên cạnh BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Tìm diện tích lớn nhất của hình chữ nhật MNPQ
- A \(1250\sqrt 3 \)
- B \(\dfrac{{625\sqrt 3 }}{2}\)
- C \(\dfrac{{625\sqrt 3 }}{4}\)
- D \(625\sqrt 3 \)
Phương pháp giải:
Dựa vào công thức tính diện tích và bất đẳng thức Cô – si để tính.
Lời giải chi tiết:
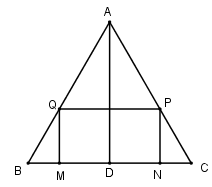
Vẽ đường cao AD của tam giác ABC. Ta có:
\(\left\{ \begin{array}{l}\frac{{AQ}}{{AB}} = \frac{{QP}}{{BC}}\\\frac{{BQ}}{{AB}} = \frac{{QM}}{{AD}}\end{array} \right. \Rightarrow \frac{{QP}}{{BC}} + \frac{{QM}}{{AD}} = \frac{{AQ}}{{AB}} + \frac{{BQ}}{{AB}} = 1\)
\( \Rightarrow 1 = {\left( {\dfrac{{QP}}{{BC}} + \dfrac{{QM}}{{AD}}} \right)^2}\mathop \ge \limits^{{\mathop{\rm Cos}\nolimits} i} 4\dfrac{{QP.QM}}{{BC.AD}} = \dfrac{{4{S_{MNPQ}}}}{{BC.AD}} \Rightarrow {S_{MNPQ}} \le \dfrac{{BC.AD}}{4} = \dfrac{{100.\dfrac{{100\sqrt 3 }}{2}}}{4} = 1250\sqrt 3 \)
Chọn A.







