Phương pháp giải:

Đặt AB = 2x, tìm mối liên hệ giữa x và a để tìm x, tính các yếu tố cần thiết và áp dụng công thức tính thể tích khối lăng trụ V = B.h trong đó B là diện tích đáy và h là chiều cao của lăng trụ.

Lời giải chi tiết:

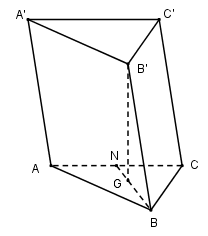
Gọi G là trọng tâm tam giác ABC. \(B'G \bot \left( {ABC} \right) \Rightarrow \widehat {\left( {BB',\left( {ABC} \right)} \right)} = \widehat {B'BG} = {60^o}\)

Đặt \(AB = 2x \Rightarrow AC = 2x.\cos 60 = x,BC = 2x.\sin 60 = x\sqrt 3 \).

Gọi \(BG \cap AC = \left\{ N \right\} \Rightarrow BG = BB'.\cos 60 = \dfrac{a}{2},BN = \dfrac{3}{2}BG = \dfrac{{3a}}{4}\)

Xét tam giác vuông BCN  có \(B{C^2} + C{N^2} = B{N^2} \Leftrightarrow 3{x^2} + \dfrac{{{x^2}}}{4} = \dfrac{{9{a^2}}}{{16}} \Leftrightarrow 52{x^2} = 9{a^2} \Rightarrow {x^2} = \dfrac{{9{a^2}}}{{52}}\)

\(\begin{array}{l}B'G = \dfrac{{\sqrt 3 }}{2}BB' = \dfrac{{a\sqrt 3 }}{2}\\ \Rightarrow V = \dfrac{1}{3}B'G.{S_{ABC}} = \dfrac{1}{3}B'G.\dfrac{1}{2}AC.BC = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{2}{x^2} = \dfrac{{9{a^3}}}{{208}}\end{array}\)

Chọn A.