Phương pháp giải:

ABCD là hình thoi nên \({S_{ABCD}} = 2{S_{ABC}} \Rightarrow {V_{S.ABCD}} = 2{V_{S.ABC}}\)

Đổi đỉnh và xác định chiều cao của hình chóp S.ABC. Tính thể tích khối chóp và tìm GTLN của thể tích khối chóp S.ABC.

Lời giải chi tiết:

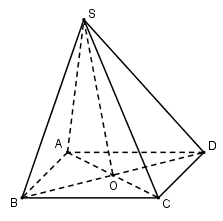
Gọi \(AC \cap BD = \left\{ O \right\} \Rightarrow \Delta SBD\) cân tại S có SO là trung tuyến \( \Rightarrow SỐ \bot BD\)

Lại có ABCD là hình thoi nên \(AC \bot BD \Rightarrow BD \bot \left( {SAC} \right)\)

Ta có: \(S{O^2} = S{B^2} - B{O^2} = A{B^2} - B{O^2} = A{O^2} \Rightarrow SO = OA = OC \Rightarrow \Delta SAC\) vuông tại S

\(\begin{array}{l}A{C^2} = {x^2} + {18^2} \Rightarrow 4O{A^2} = {x^2} + {18^2}\\{V_{S.ABCD}} = 2{V_{S.ABC}} = 2.\dfrac{1}{3}.BO.{S_{SAC}} = 2.\dfrac{1}{3}.\dfrac{1}{2}.OB.SA.SC\\ = \dfrac{1}{3}.\sqrt {A{B^2} - O{A^2}} .SA.SC = \dfrac{1}{3}.\sqrt {{{18}^2} - \dfrac{{{x^2} + {{18}^2}}}{4}} .x.18 = 6x\sqrt {243 - \dfrac{1}{4}{x^2}} \\ = 12.\dfrac{1}{2}x.\sqrt {243 - \dfrac{1}{4}{x^2}} \mathop \le \limits^{{\mathop{\rm Cos}\nolimits} i} 6.\left( {\dfrac{1}{4}{x^2} + 243 - \dfrac{1}{4}{x^2}} \right) = 1458\end{array}\)

 Dấu  xảy ra \( \Leftrightarrow \dfrac{1}{2}x = \sqrt {243 - \frac{1}{4}{x^2}}  \Leftrightarrow x = 9\sqrt 6 \left( {do {\rm{ }}x > 0} \right)\)

Chọn B.