Câu hỏi
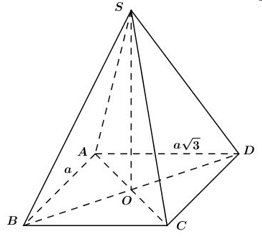
Cho hình chóp S.ABCD đáy là hình chữ nhật tâm O; \(AB = a\),\(AD = a\sqrt 3 \), \(SA = 3a\), \(SO\) vuông góc với mặt đáy ( ABCD). Thể tích khối chóp S.ABC bằng:
- A \({a^3}\sqrt 6 \)
- B \(\frac{{2{a^3}\sqrt 6 }}{3}\)
- C \(\frac{{{a^3}\sqrt 6 }}{3}\)
- D \(2{a^3}\sqrt 6 \)
Phương pháp giải:
+) SO vuông góc với mặt phẳng (ABCD) nên SO là chiều cao của khối chóp SABCD đồng thời là khối chóp của khối chóp SABC.
+) Công thức tính thể tích: \({V_{SABC}} = \frac{1}{3}.SO.{S_{ABC}} = \frac{1}{3}.SO.\frac{1}{2}.AB.BC = \frac{1}{6}.SO.AB.BC\) (do \(\Delta ABC\) vuông tại B).
+) Sử dụng định lý Pi-ta-go ứng với các tam giác vuông để tính chiều cao SO.
Lời giải chi tiết:
Áp dụng định lý Pi-ta-go cho tam giác ABC vuông tại A ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + 3{a^2}} = 2a.\)
O là tâm hình chữ nhật \( \Rightarrow AO = \frac{1}{2}AC = a.\)
Áp dụng định lý Pi-ta-go cho tam giác vuông SAO vuông tại O ta có:
\(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {9{a^2} - {a^2}} = 2\sqrt 2 a.\)
\( \Rightarrow {V_{SABC}} = \frac{1}{6}.SO.AB.BC = \frac{1}{6}.2a\sqrt 2 .a.a\sqrt 3 = \frac{{{a^3}\sqrt 6 }}{3}.\)
Chọn C.