Phương pháp giải:

Cô lập k, đưa phương trình về dạng \(f\left( x \right) < f\left( k \right)\), khi đó phương trình luôn đúng với mọi \(x \in \left( {0;\frac{\pi }{2}} \right) \Leftrightarrow f\left( k \right) \ge \mathop {\max }\limits_{\left( {0;\frac{\pi }{2}} \right)} f\left( x \right)\).

Lời giải chi tiết:

\(\frac{1}{{{{\sin }^2}x}} < \frac{1}{{{x^2}}} + 1 - \frac{k}{{{\pi ^2}}} \Rightarrow f\left( x \right) = \frac{1}{{{{\sin }^2}x}} - \frac{1}{{{x^2}}} < 1 - \frac{k}{{{\pi ^2}}}\,\,\,\forall x \in \left( {0;\frac{\pi }{2}} \right) \Rightarrow 1 - \frac{k}{{{\pi ^2}}} \ge \mathop {\max }\limits_{\left( {0;\frac{\pi }{2}} \right)} f\left( x \right)\)

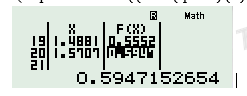
Sử dụng máy tính cầm tay, chức năng [MODE] [7], nhập hàm số \(f\left( x \right) = \frac{1}{{{{\sin }^2}x}} - \frac{1}{{{x^2}}}\), start = 0, end = \(\frac{\pi }{2}\)

\(step = \frac{{\frac{\pi }{2}}}{{19}}\)  (nhớ đổi đơn vị sang radian) ta được:  

\( \Rightarrow \mathop {\max }\limits_{\left( {0;\frac{\pi }{2}} \right)} f\left( x \right) = f\left( {\frac{\pi }{2}} \right) = 1 - \frac{4}{{{\pi ^2}}} \le 1 - \frac{k}{{{\pi ^2}}} \Rightarrow \frac{k}{{{\pi ^2}}} \le \frac{4}{{{\pi ^2}}} \Rightarrow k \le 4.\)

Chọn C.