Câu hỏi
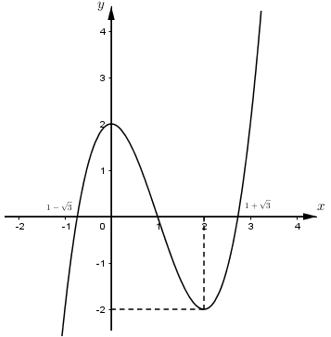
Cho hàm số \(f\left( x \right)={{x}^{3}}-3{{x}^{2}}+2\) có đồ thị là đường cong trong hình bên.
Hỏi phương trình \({{\left( {{x}^{3}}-3{{x}^{2}}+2 \right)}^{3}}-3{{\left( {{x}^{3}}-3{{x}^{2}}+2 \right)}^{2}}+2=0\) có bao nhiêu nghiệm thực dương phân biệt?
- A 3
- B 5
- C 7
- D 1
Phương pháp giải:
Đặt \(t={{x}^{3}}-3{{x}^{2}}+2=f\left( x \right)\), dựa vào đồ thị hàm số đã cho tìm ra các nghiệm \({{t}_{i}}\).
Xét các phương trình \(f\left( x \right)={{t}_{i}}\), số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y=f\left( x \right)\) và đường thẳng \(y={{t}_{i}}\) song song với trục hoành.
Lời giải chi tiết:
Cách giải:
Đặt \(t={{x}^{3}}-3{{x}^{2}}+2=f\left( x \right)\) khi đó phương trình trở thành \({{t}^{3}}-3{{t}^{2}}+2=0\) và hàm số \(f\left( t \right)={{t}^{3}}-3{{t}^{2}}+2\) có hình dáng y như trên. Dựa vào đồ thị hàm số ta thấy \(f\left( t \right)=0\Leftrightarrow \left[ \begin{align} & t=1-\sqrt{3} \\ & t=1 \\ & t=1+\sqrt{3} \\\end{align} \right.\)
Với \(t=1+\sqrt{3}\Rightarrow f\left( x \right)=1+\sqrt{3}\,\,\,\left( 1 \right)\). Số nghiệm của phương trình (1) là số giao điểm của đồ thị hàm số \(y=f\left( x \right)\) và đường thẳng \(y=1+\sqrt{3}\) song song với trục hoành.
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y=1+\sqrt{3}\) cắt đồ thị hàm số \(y=f\left( x \right)\) tại 1 điểm có hoành độ dương duy nhất nên phương trình (1) có 1 nghiệm dương duy nhất.
Với \(t=1\Rightarrow f\left( t \right)=1\,\,\,\left( 2 \right)\). Lập luận tương tự như trên ta thấy phương trình (2) có 2 nghiệm dương phân biệt.
Với \(t=1-\sqrt{3}\Rightarrow f\left( t \right)=1-\sqrt{3}\,\,\,\left( 3 \right)\). Phương trình 3 có 2 nghiệm dương phân biệt.
Vậy phương trình ban đầu có 5 nghiệm dương phân biệt.
Chọn B.