Câu hỏi
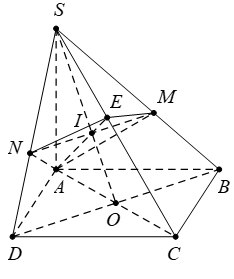
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và có thể tích \(V.\) Gọi \(E\) là điểm trên cạnh \(SC\) sao cho \(EC=2\,ES.\) Gọi \(\left( \alpha \right)\) là mặt phẳng chứa đường thẳng \(AE\) và song song với đường thẳng \(BD,\) \(\left( \alpha \right)\) cắt hai cạnh \(SB,\,\,SD\) lần lượt tại hai điểm \(M,\,\,N.\) Tính theo \(V\) thể tích khối chóp \(S.AMEN.\)
- A \(\frac{V}{6}.\)
- B \(\frac{V}{27}.\)
- C \(\frac{V}{9}.\)
- D \(\frac{V}{12}.\)
Phương pháp giải:
Dùng định lí Thalet và phương pháp tỉ số thể tích để tính thể tích khối chóp cần tìm
Lời giải chi tiết:
Gọi \(O\) là tâm của hình bình hành \(ABCD\) và \(I=SO\cap AE.\)
Ba điểm \(E,A,I\) thẳng hàng nên áp dụng định lý Menelaus cho tam giác \(SOC\) ta có: \(\frac{SE}{EC}.\frac{CA}{AO}.\frac{OI}{IS}=1\Rightarrow \frac{OI}{SI}=1\Rightarrow \frac{SI}{SO}=\frac{1}{2}.\)
Vì \(MN\)//\(BD\)\(\Rightarrow \)\(\frac{SM}{SB}=\frac{SN}{SD}=\frac{SI}{SO}=\frac{1}{2}\) (định lí Thalet).
Do đó \(\frac{{{V}_{S.AME}}}{{{V}_{S.ABC}}}=\frac{SM}{SB}.\frac{SE}{SC}=\frac{1}{2}.\frac{1}{3}=\frac{1}{6}\Rightarrow {{V}_{S.AME}}=\frac{V}{12}\);
Tương tự, ta có \({{V}_{S.ANE}}=\frac{V}{12}.\) Vậy \({{V}_{S.AMEN}}={{V}_{S.AME}}+{{V}_{S.ANE}}=\frac{V}{12}+\frac{V}{12}=\frac{V}{6}.\)
Chọn A