Câu hỏi
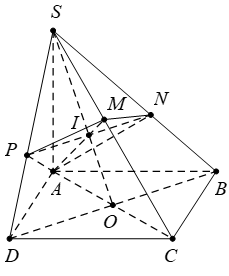
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Điểm \(M\) di động trên cạnh \(SC,\) đặt \(\frac{MC}{MS}=k.\) Mặt phẳng qua \(A,\,\,M\) song song với \(BD\) cắt \(SB,\,\,SD\) thứ tự tại \(N,\,\,P.\) Thể tích khối chóp \(C.APMN\) lớn nhất khi
- A \(k=\sqrt{3}.\)
- B \(k=1.\)
- C \(k=2.\)
- D \(k=\sqrt{2}.\)
Phương pháp giải:
Dùng định lí Thalet, định lý Menelaus và phương pháp tỉ số thể tích để tính thể tích khối chóp theo tham số k. Khảo sát hàm số chứa biến k để tìm giá trị lớn nhất – giá trị nhỏ nhất
Lời giải chi tiết:
Lời giải:
Gọi \(O\) là tâm của hình bình hành \(ABCD\) và \(I=SO\cap AM.\)
Ba điểm \(M,A,I\) thẳng hàng nên áp dụng định lý Menelaus cho tam giác $SOC$ ta có: \(\frac{SM}{MC}.\frac{CA}{AO}.\frac{OI}{IS}=1\Rightarrow \frac{OI}{SI}=\frac{k}{2}.\)
Vì \(NP\)//\(BD\)\(\Rightarrow \)\(\frac{SP}{SD}=\frac{SI}{SO}=\frac{SN}{SB}=\frac{2}{k+2}\) (định lí Thalet).
Và \(d\left( P;\left( ABCD \right) \right)=d\left( N;\left( ABCD \right) \right)=\frac{DP}{SD}d\left( S;\left( ABCD \right) \right)\)
\(=\frac{k}{k+2}.\,d\left( S;\left( ABCD \right) \right)\Rightarrow {{V}_{P.ACD}}={{V}_{N.ABC}}=\frac{k}{2k+4}.{{V}_{S.ABCD}}.\)
Ta có \(\frac{{{V}_{S.AMP}}}{{{V}_{S.ACD}}}=\frac{SM}{SC}.\frac{SP}{SD}=\frac{1}{k+1}.\frac{2}{k+2}\Rightarrow {{V}_{S.ANMP}}=\frac{2}{\left( k+1 \right)\left( k+2 \right)}.{{V}_{S.ABCD}}\)
Vậy \({{V}_{C.ANMP}}={{V}_{S.ABCD}}-{{V}_{S.ANMP}}-{{V}_{P.ACD}}-{{V}_{N.ABC}}=\left( 1-\frac{2}{\left( k+1 \right)\left( k+2 \right)}-\frac{k}{k+2} \right).{{V}_{S.ABCD}}\)\(=\frac{2k}{{{k}^{2}}+3k+2}.{{V}_{S.ABCD}}\)
Để \({{\left\{ {{V}_{C.ANMP}} \right\}}_{\max }}\Leftrightarrow f\left( k \right)=\frac{k}{{{k}^{2}}+3k+2}\) đạt giá trị lớn nhất.
Xét hàm số \(f\left( k \right)=\frac{k}{{{k}^{2}}+3k+2}\) trên khoảng \(\left( 0;+\,\infty \right)\) có:
\(f'\left( k \right)=\frac{-{{k}^{2}}+2}{{{\left( {{k}^{2}}+3k+2 \right)}^{2}}}=0\Leftrightarrow k=\sqrt{2}\) (vì \(k>0\))
\(\Rightarrow \)\(\underset{\left( 0;+\,\infty \right)}{\mathop{\max }}\,f\left( k \right)=f\left( \sqrt{2} \right)=3-2\sqrt{2}.\)
Dấu bằng xảy ra khi và chỉ khi \(k=\sqrt{2}.\) Vậy khi \(k=\sqrt{2}\) thì thể tích khối chóp \(C.ANMP\) lớn nhất.
Chọn D