Câu hỏi
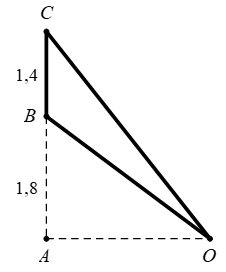
Một màn ảnh hình chữ nhật cao \(1,4m\) được đặt ở độ cao \(1,8m\) so với tầm mắt (tính đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu sao cho góc nhìn lớn nhất. Hãy xác định khoảng cách đó.
- A \(2,4\,\,m.\)
- B \(2,42\,\,m.\)
- C \(2,46\,\,m.\)
- D \(2,21\,\,m.\)
Phương pháp giải:
Dựa vào hệ thức lượng trong tam giác và công thức lượng giác xác định độ lớn của góc cần tính thông qua khoảng cách. Khảo sát hàm số tìm min – max
Lời giải chi tiết:
Lời giải:
Với bài toán này, ta cần xác định \(OA\) để góc \(\widehat{BOC}\) lớn nhất. Điều này xảy ra \(\Leftrightarrow \)\(\tan \widehat{BOC}\) lớn nhất.
Đặt \(OA=x\,\,\,\left( m \right)\) với \(x>0.\) Ta có:
\(\tan \widehat{BOC}=\tan \left( \widehat{AOC}-\widehat{AOB} \right)=\frac{\tan \widehat{AOC}-\tan \widehat{AOB}}{1+\tan \widehat{AOC}.tan\widehat{AOB}}\)\(=\frac{\frac{AC}{OA}-\frac{AB}{OA}}{1+\frac{AC.AB}{O{{A}^{2}}}}=\frac{\frac{1,4}{x}}{1+\frac{3,2.1,8}{{{x}^{2}}}}=\frac{1,4x}{{{x}^{2}}+5,76}.\)
Xét hàm số \(f\left( x \right)=\frac{1,4x}{{{x}^{2}}+5,76}\) trên \(\left( 0;+\,\infty \right),\) có:
\({f}'\left( x \right)=\frac{-\,1,4{{x}^{2}}+1,4.5,76}{{{\left( {{x}^{2}}+5,76 \right)}^{2}}};\,\,{f}'\left( x \right)=0\Leftrightarrow \left\{ \begin{align} & x>0 \\ & {{x}^{2}}=5,76 \\\end{align} \right.\Leftrightarrow x=2,4.\)
Tính các giá trị \(f\left( 0 \right)=0;\,\,f\left( 2,4 \right)=\frac{7}{24};\,\,\underset{x\,\to \,+\,\infty }{\mathop{\lim }}\,f\left( x \right)=0\) suy ra \(\underset{\left( 0;+\,\infty \right)}{\mathop{\max }}\,f\left( x \right)=\frac{7}{24}.\)
Vậy khoảng cách \(OA\) cần tìm là \(2,4\,\,m.\)
Chọn A