Phương pháp giải:

Lập hàm số chi phí theo một ẩn sau đó tìm giá trị nhỏ nhất của hàm số đó.

Lời giải chi tiết:

Gọi a là chiều dài cạnh đáy hình vuông của hình hộp chữ nhật và b là chiều cao của hình hộp chữ nhật ta có \({{a}^{2}}b=8\) \(\left( a,b>0 \right)\Rightarrow ab=\frac{8}{a}\).

Diện tích đáy hình hộp là \({{a}^{2}}\) và diện tích xung quanh là \(4ab\) nên chi phí để làm thùng tôn là:

\(f(a)=100{{a}^{2}}+50.4ab=100{{a}^{2}}+200ab=100{{a}^{2}}+200.\frac{8}{a}\)

\(=100{{a}^{2}}+\frac{1600}{a}=100\left( {{a}^{2}}+\frac{16}{a} \right)\) (nghìn đồng).

Cách 1:

\(f'(a) = 200a - \frac{{1600}}{{{a^2}}} = 0 \Leftrightarrow 200{a^3} = 1600 \Leftrightarrow {a^3} = 8 \Leftrightarrow a = 2\).

Bảng biến thiên:

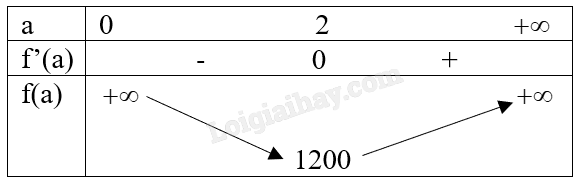
Vậy chi phí nhỏ nhất bằng 1 200 000 đồng khi và chỉ khi cạnh đáy hình hộp bằng 2m.

Cách 2:

Áp dụng BĐT Cauchy ta có \({{a}^{2}}+\frac{16}{a}={{a}^{2}}+\frac{8}{a}+\frac{8}{a}\ge 3\sqrt(3){{{a}^{2}}.\frac{8}{a}.\frac{8}{a}}=3.4=12\).

Dấu bằng xảy ra khi và chỉ khi \({{a}^{2}}=\frac{8}{a}\Leftrightarrow a=2\).

Vậy chi phí nhỏ nhất bằng 1 200 000 đồng khi và chỉ khi cạnh đáy hình hộp bằng 2m.