Câu hỏi
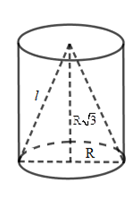
Cho hình trụ có hai đáy là hai hình tròn \(\left( O \right)\) và \(\left( {O'} \right)\), chiều cao \(R\sqrt 3 \), bán kính đáy \(R\) và hình nón có đỉnh là \(O'\), đáy là hình tròn \(\left( {O;R} \right)\). Tính tỉ số giữa diện tích xung quanh của hình trụ và diện tích xung quanh của hình nón.
- A \(2\)
- B \(3\)
- C \(\sqrt 2 \)
- D \(\sqrt 3 \)
Phương pháp giải:
Công thức tính diện tích xung quanh hình trụ: \({S_{xq}} = 2\pi Rh\).
Công thức tính diện tích xung quanh hình nón: \({S_{xq}} = \pi Rl\).
Lời giải chi tiết:
Diện tích xung quanh hình trụ là:
\({S_1} = 2\pi Rh = 2\pi R.R\sqrt 3 = 2\pi {R^2}\sqrt 3 \).
Độ dài đường sinh của hình nón: \(l = \sqrt {{R^2} + {h^2}} = \sqrt {{R^2} + 3{R^2}} = 2R\).
Diện tích xung quanh hình nón: \({S_2} = \pi Rl = \pi R.2R = 2\pi {R^2}\).
Vậy \(\frac{{{S_1}}}{{{S_2}}} = \frac{{2\pi {R^2}\sqrt 3 }}{{2\pi {R^2}}} = \sqrt 3 \).
Câu hỏi trước
