Câu hỏi
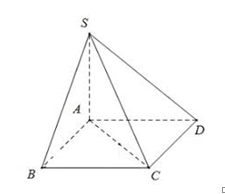
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(AB = a,AD = 2a\) , cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng \(\frac{{2{a^3}}}{3}\) . Tính số đo góc giữa đường thẳng SB với mặt phẳng (ABCD).
- A \({30^0}\)
- B \({60^0}\)
- C \({45^0}\)
- D \({75^0}\)
Phương pháp giải:
Thể tích khối chóp \(V = \frac{1}{3}{S_d}.h\) : h là chiều cao của khối chóp, S là diện tích đáy.
Phương pháp xác định góc giữa đường thẳng và mặt phẳng: Góc giữa đường thẳng và mặt phẳng chính là góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng.
Lời giải chi tiết:
Ta có:
\(SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB,AB} \right)} = \widehat {SBA}\)
Ta có: \(V = \frac{1}{3}SA.{S_{ABCD}} \Rightarrow SA = \frac{{3V}}{{{S_{ABCD}}}} = \frac{{3.\frac{{2{a^3}}}{3}}}{{a.2a}} = a\)
Trong tam giác SAB vuông tại A ta có: \(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = 1 \Rightarrow \widehat {SBA} = {45^0}\)