Câu hỏi
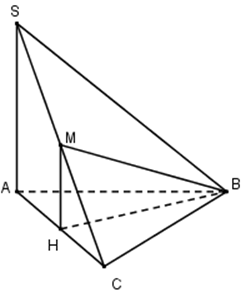
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh SA vuông góc với mặt phẳng đáy và \(SA=2a\). Gọi M là trung điểm của SC. Tính cosin của góc \(\alpha \) là góc giữa đường thẳng BM và mặt phẳng (ABC).
- A \(\cos \alpha =\frac{\sqrt{7}}{14}\)
- B \(\cos \alpha =\frac{2\sqrt{7}}{7}\)
- C \(\cos \alpha =\frac{\sqrt{5}}{7}\)
- D \(\cos \alpha =\frac{\sqrt{21}}{7}\)
Phương pháp giải:
Phương pháp:
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó
Lời giải chi tiết:
Cách giải:
Gọi H là trung điểm của AC ta có HM // SA nên \(HM\bot \left( ABC \right)\), khi đó \(\left( MB;\left( ABC \right) \right)=\left( MB;HB \right)=\widehat{MBH}\)
Ta có : \(SC=\sqrt{4{{a}^{2}}+{{a}^{2}}}=a\sqrt{5}=SB\)
Xét tam giác SBC có
\(M{{B}^{2}}=\frac{S{{B}^{2}}+B{{C}^{2}}}{2}-\frac{S{{C}^{2}}}{4}=\frac{5{{a}^{2}}+{{a}^{2}}}{2}-\frac{5{{a}^{2}}}{4}=\frac{7{{a}^{2}}}{4}\Leftrightarrow BM=\frac{a\sqrt{7}}{2}\)
Tam giác ABC đều cạnh a nên \(BH=\frac{a\sqrt{3}}{2}\)
Xét tam giác vuông BHM có: \(\cos \widehat{MBH}=\frac{BH}{BM}=\frac{\frac{a\sqrt{3}}{2}}{\frac{a\sqrt{7}}{2}}=\frac{\sqrt{21}}{7}\)
Chọn D.