Phương pháp giải:

Hình chóp có các cạnh bên bằng nhau thì chân đường cao hạ từ đỉnh trùng với tâm đường tròn ngoại tiếp đáy.

Lời giải chi tiết:

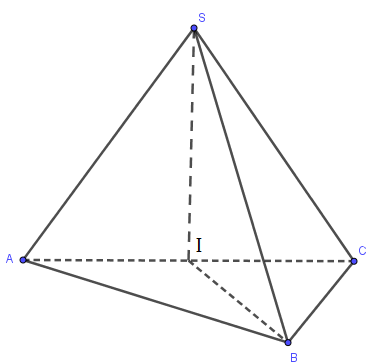
Hình chóp \(S.ABC\) có \(SA=SB=SC\) nên chân đường vuông góc kẻ từ S tới đáy là tâm đường tròn ngoại tiếp tam giác ABC.

Đặt độ dài \(SA=SB=SC=a\)

\(\Delta \)SAB vuông cân tại S, SA = SB = a \(\Rightarrow AB=a\sqrt{2}\)

\(\Delta \)SBC cân tại S có \(\,\widehat{BSC}={{60}^{0}}\) => \(\Delta \)SBC đều => BC = SB = SC = a

\(\Delta \)SAC cân tại S có\(\,\widehat{ASC}={{120}^{0}}\) . Áp dụng định lý Côsin, ta có:

\(AC=\sqrt{S{{A}^{2}}+S{{C}^{2}}-2.SA.SC.\cos {{120}^{0}}}=\sqrt{{{a}^{2}}+{{a}^{2}}-2.a.a.\frac{-1}{2}}=a\sqrt{3}\)

Xét \(\Delta \)ABC, ta thấy: \(A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}\)

=> \(\Delta \)ABC vuông tại B.

Do đó, tâm đường tròn ngoại tiếp \(\Delta \)ABC là trung điểm của cạnh AC (ta gọi điểm đó là I)

Suy ra, \(SI\bot (ABC)\)

=> BI là hình chiếu của SB trên (ABC)

=> \(\left( SB;(ABC) \right)=(SB;IB)=\widehat{SBI}\)

Xét \(\Delta \)ABC: \(BI=\frac{AC}{2}=\frac{a\sqrt{3}}{2}\)

Xét \(\Delta \)SBI có:  \(\cos \,\widehat{SBI}=\frac{BI}{SB}=\frac{\frac{a\sqrt{3}}{2}}{a}=\frac{\sqrt{3}}{2}\Rightarrow \widehat{SBI}={{30}^{0}}\) => \(\left( SB;(ABC) \right)={{30}^{0}}\)

Chọn D.