Câu hỏi
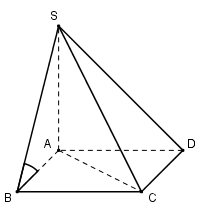
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, góc giữa cạnh SB và mặt đáy bằng \(45^0\). Độ dài cạnh SC bằng:
- A \(\dfrac{a}{2}\)
- B \(\dfrac{{a\sqrt 3 }}{2}\)
- C \(a\sqrt 3 \)
- D \(\dfrac{{a\sqrt 3 }}{3}\)
Phương pháp giải:
Xác định góc giữa SB và mặt đáy, sử dụng định lí Pi – ta – go để tính SC.
Lời giải chi tiết:
Do \(SA \bot \left( {ABCD} \right) \Rightarrow \) A là hình chiếu của S trên (ABCD) \( \Rightarrow AB\) là hình chiếu của SB trên (ABCD)
\( \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} = {45^0}.\) Suy ra tam giác SAB vuông cân tại A nên SA = AB = a.
ABCD là hình vuông cạnh a nên \(AC = a\sqrt 2 \).
Xét tam giác vuông SAC có \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {{a^2} + 2{a^2}} = a\sqrt 3 \).
Chọn C.
Câu hỏi trước
