Câu hỏi
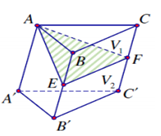
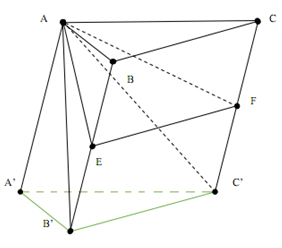
Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(E,F\) lần lượt là trung điểm của \(BB'\) và \(CC'\). Mặt phẳng \(\left( {AEF} \right)\) chia khối lăng trụ thành hai phần có thể tích \({V_1}\) và \({V_2}\) như hình vẽ. Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) là
- A \(1\)
- B \(\frac{1}{3}\)
- C \(\frac{1}{4}\)
- D \(\frac{1}{2}\)
Phương pháp giải:
Tính thể tích các khối đa diện theo thể tích khối lăng trụ \(ABC.A'B'C'\) rồi tính tỉ số thể tích \(\frac{{{V_1}}}{{{V_2}}}\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}{V_{A.A'B'C'}} = \frac{1}{3}{S_{A'B'C'}}.h = \frac{1}{3}{V_{ABC.A'B'C'}}\\ \Rightarrow {V_{A.BCC'B'}} = {V_{ABC.A'B'C'}} - {V_{A.A'B'C'}} = \frac{2}{3}{V_{ABC.A'B'C'}}\end{array}\)
Mà \({S_{BCFE}} = \frac{1}{2}{S_{BCC'B'}}\)
\( \Rightarrow {V_{A.BCFE}} = \frac{1}{2}{V_{BCC'B'}} = \frac{1}{2}.\frac{2}{3}{V_{ABC.A'B'C'}} = \frac{1}{3}{V_{ABC.A'B'C'}}\) \(\begin{array}{l} \Rightarrow {V_{AEF.A'B'C'}} = {V_{ABC.A'B'C'}} - {V_{A.BCFE}} = \frac{2}{3}{V_{ABC.A'B'C'}}\\ \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{{{V_{A.BCFE}}}}{{{V_{AEF.A'B'C'}}}} = \frac{1}{2}\end{array}\)
Chọn D.