Câu hỏi
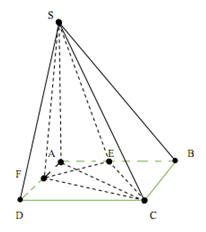
Cho hình chóp \(S.ABC{\rm{D}}\) có thể tích \(V\) đáy \(ABCD\) là hình bình hành. Gọi \(E,F\) lần lượt là trung điểm của các cạnh \(AB\) và \(AD\). Thể tích của khối chóp \(S.AECF\) là
- A \(\frac{V}{2}\)
- B \(\frac{V}{4}\)
- C \(\frac{V}{3}\)
- D \(\frac{V}{6}\)
Phương pháp giải:
Tính tỉ số diện tích hai đáy \(AECF\) và \(ABCD\), từ đó suy ra tỉ số thể tích của hai khối chóp.
Lời giải chi tiết:
Dễ thấy: \({S_{A{\rm{E}}C}} = \frac{1}{2}{S_{ABC}} = \frac{1}{4}{S_{ABC{\rm{D}}}}\)
\( \Rightarrow {S_{A{\rm{E}}CF}} = {S_{AEC}} + {S_{AFC}} = \frac{1}{2}{S_{ABC{\rm{D}}}}\)
\( \Rightarrow {V_{S.A{\rm{E}}CF}} = \frac{1}{2}{V_{S.ABC{\rm{D}}}}\)
Câu hỏi trước
