Câu hỏi
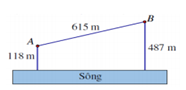
Cho hai vị trí \(A,B\) cách nhau,cùng nằm về một phía bờ sông như hình vẽ. Khoảng cách từ \(A\) và từ \(B\) đến bờ sông lần lượt là 118m và 487km. Một người đi từ \(A\) đến bờ sông để lấy nước mang về \(B\). Đoạn đường ngắn nhất mà người đó có thể đi là:
- A \(569,5m\)
- B \(671,4m\)
- C \(779,8m\)
- D \(741,2m\)
Phương pháp giải:
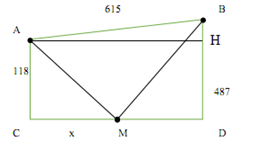
Gọi độ dài \(MC = x\), viết biểu thức tính độ đài quãng đường đi từ \(A\) đến \(M\) rồi từ \(M\) đến \(B\) theo ẩn \(x\).
Xét hàm số \(y = f\left( x \right)\) vừa có ở trên và tìm GTNN.
Lời giải chi tiết:
Đặt \(CM = x\left( {x > 0} \right)\)
Dễ tính ra \(CD = AH = \sqrt {{{615}^2} - {{\left( {487 - 118} \right)}^2}} = 492\)
Từ đề bài ta có: \(f\left( x \right) = \sqrt {{x^2} + {{118}^2}} + \sqrt {{{\left( {492 - x} \right)}^2} + {{487}^2}} \)
Quãng đường ngắn nhất người đó có thể đi là giá trị nhỏ nhất của \(f\left( x \right)\) trên \(\left[ {0;492} \right]\)
Ta có: \(f'\left( x \right) = \frac{{2{\rm{x}}}}{{2\sqrt {{x^2} + {{118}^2}} }} - \frac{{2\left( {492 - x} \right)}}{{2\sqrt {{{\left( {492 - x} \right)}^2} + {{487}^2}} }}\)
\( \Rightarrow f'\left( x \right) = 0\)
\( \Leftrightarrow x\sqrt {{{\left( {492 - x} \right)}^2} + {{487}^2}} - \left( {492 - x} \right)\sqrt {{x^2} + {{118}^2}} = 0\)
\( \Leftrightarrow {\left( {492 - x} \right)^2}\left( {{x^2} + {{118}^2}} \right) = {x^2}\left( {{{\left( {492 - x} \right)}^2} + {{487}^2}} \right)\)\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{{58056}}{{605}} \in \left[ {0;492} \right]\\x = - \frac{{472}}{3} \notin \left[ {0;492} \right]\end{array} \right.\)
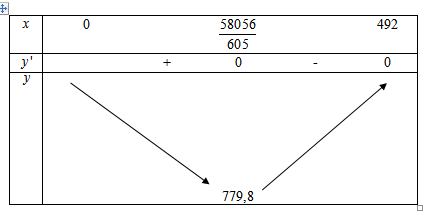
Ta có bảng biến thiên
Vậy quãng đường ngắn nhất mà người đó có thể đi là 779,8.