Phương pháp giải:

Phương pháp tìm GTLN, GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {a;b} \right]\):

- Tính \(y'\), tìm các nghiệm \({x_1},{x_2},...,{x_n}\)của phương trình \(y' = 0\) mà \(a \le {x_1} < {x_2} < ... < {x_n} \le b\) .

- Tính các giá trị \(f\left( a \right),f\left( {{x_1}} \right),...,f\left( {{x_n}} \right),f\left( b \right)\).

- So sánh các giá trị trên và kết luận.

Lời giải chi tiết:

Ta có: \(y' = 4{{\rm{x}}^3} + 4{\rm{x}}\)\( \Rightarrow y' = 0 \Leftrightarrow x = 0\)

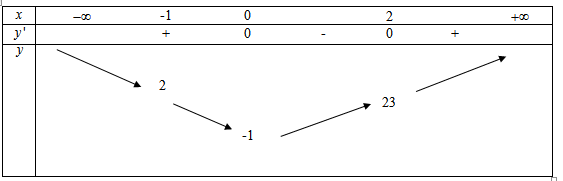
Ta có bảng biến thiên

Từ bảng biến thiên ta thấy \(M = 23,m = - 1 \Rightarrow M.m = 23.\left( { - 1} \right) = - 23\)