Phương pháp giải:

Khảo sát hàm số \(y = f\left( x \right)\) trên TXĐ và rút ra kết luận.

Lời giải chi tiết:

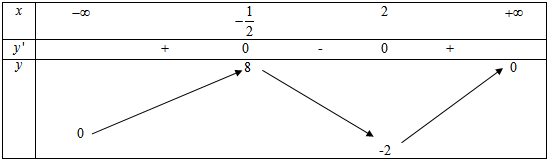
Ta có: \(f'\left( x \right) = \frac{{8{{\rm{x}}^2} - 12{\rm{x}} - 8}}{{{{\left( {{x^2} + 1} \right)}^2}}}\)

\(f'\left( x \right) = 0 \Leftrightarrow x = 2\) hoặc \(x =  - \frac{1}{2}\)

\(\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  - \infty } y = 0\)

Bảng biến thiên

Vậy giá trị lớn nhất của hàm số là \(y = 8\) tại \(x =  - \frac{1}{2}\)