Phương pháp giải:

- Khảo sát hàm số \(y =  - {x^4} + 6{x^2} - 5\) tìm điểm cực tiểu của đồ thị hàm số.

- Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm cực tiểu vừa tìm được.

Lời giải chi tiết:

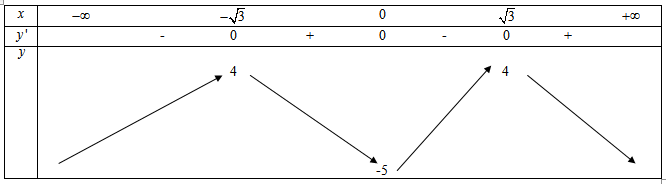
Ta có: \(y' =  - 4{{\rm{x}}^3} + 12{\rm{x}}\)

\( \Rightarrow y' = 0 \Leftrightarrow x = 0\) hoặc \(x = \sqrt 3 \) hoặc \(x =  - \sqrt 3 \)

Ta có bảng biến thiên

Vậy phương trình đường tiếp tuyến tại điểm cực tiểu của đồ thị hàm số là \(y =  - 5\)