Câu hỏi
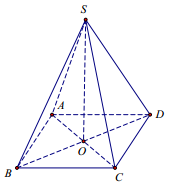
Cho khối chóp tứ giác đều \(S.ABC{\rm{D}}\) có cạnh bằng a, cạnh bên SC tạo với mặt đáy một góc \(45^\circ \). Tính thể tích của khối chóp \(S.ABC{\rm{D}}\)
- A \(V = \dfrac{{\sqrt 2 {a^3}}}{3}\)
- B \(V = \dfrac{{\sqrt 2 {a^3}}}{6}\)
- C \(V = \dfrac{{2{a^3}}}{3}\)
- D \(V = 2{{\rm{a}}^3}\)
Phương pháp giải:
Xác định góc giữa đường thẳng \(SC\) với đáy bằng cách xác định góc giữa đường thẳng \(SC\) với hình chiếu của nó trên mặt phẳng đáy.
Tính thể tích khối chóp bằng công thức \(V = \dfrac{1}{3}Sh\).
Lời giải chi tiết:
Ta có: \(\left( {SC;\left( {ABC{\rm{D}}} \right)} \right) = \widehat {SCO} = 45^\circ \)
Khi đó : \(\tan 45^\circ = 1 = \dfrac{{SO}}{{CO}} \Rightarrow SO = CO = \dfrac{{a\sqrt 2 }}{2}\)
Suy ra : \({V_{SABC{\rm{D}}}} = \dfrac{1}{3}.SO.{S_{ABC{\rm{D}}}} = \dfrac{1}{3}.\dfrac{{a\sqrt 2 }}{2}.{a^2} = \dfrac{{\sqrt 2 {a^3}}}{6}\)
Đáp án B
Câu hỏi trước
