Câu hỏi
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, I nằm trên cạnh SC sao cho IS = 2IC. Mặt phẳng (P) chứa cạnh AI cắt cạnh SB, SD lần lượt tại M, N. Gọi V’, V lần lượt là thể tích khối chóp S.AMIN và S.ABCD. Tính giá trị nhỏ nhất của tỷ số thể tích \(\dfrac{{V'}}{V}\)
- A \(\dfrac{4}{5}\)
- B \(\dfrac{5}{{54}}\)
- C \(\dfrac{8}{{15}}\)
- D \(\dfrac{5}{{24}}\)
Phương pháp giải:
Tỷ lệ thể tích của hai khối chóp nhỏ nhất ⇔ MN // BD
Lời giải chi tiết:
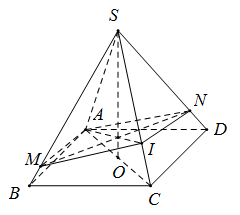
Gọi K là giao điểm của AI và SO
Ta có M, N, K thẳng hàng
\(\dfrac{{V'}}{V}\) nhỏ nhất ⇔ MN // BD
Khi MN // BD: Gọi E là trung điểm IC ⇒ OE // AI
\(\dfrac{{SK}}{{SO}} = \dfrac{{SI}}{{SE}} = \dfrac{{SI}}{{SI + \dfrac{{IC}}{2}}} = \dfrac{{2IC}}{{2IC + \dfrac{{IC}}{2}}} = \dfrac{4}{5}\)
\( \Rightarrow \dfrac{{SM}}{{SB}} = \dfrac{{SN}}{{SD}} = \dfrac{4}{5}\)
Suy ra \(\dfrac{{{V_{S.AMI}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SI}}{{SC}} = \dfrac{4}{5}.\dfrac{2}{3} = \dfrac{8}{{15}}\)
Tương tự ta có \(\dfrac{{{V_{S.ANI}}}}{{{V_{S.ADC}}}} = \dfrac{8}{{15}}\)
\( \Rightarrow \dfrac{{V'}}{V} = \dfrac{8}{{15}}\)
Chọn đáp án C







