Câu hỏi
Lăng trụ tam giác đều \(ABC.A’B’C’\) có góc giữa hai mặt phẳng \((A’BC)\) và \((ABC)\) bằng \(30^0\). Điểm \(M\) nằm trên cạnh \(AA’\). Biết cạnh \(AB = a\sqrt 3 \), thể tích khối đa diện \(MBCC’B'\) bằng:
- A \(\dfrac{{3{a^3}}}{4}\)
- B \(\dfrac{{3{a^3}\sqrt 3 }}{2}\)
- C \(\dfrac{{3{a^3}\sqrt 2 }}{4}\)
- D \(\dfrac{{2{a^3}}}{3}\)
Phương pháp giải:
Sử dụng góc giữa hai mặt phẳng để tính \(AA’\).
Chứng minh khoảng cách từ \(M\) đến (BCC’B’) bằng khoảng cách từ \(A\) đến \((BCC’B’)\).
Lời giải chi tiết:
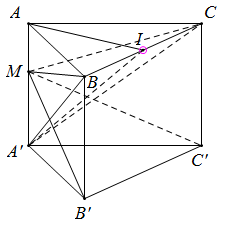
Gọi I là trung điểm BC ⇒ AI ⊥ BC
⇒ BC ⊥ (AIA’)
Góc giữa (A’BC) và (ABC) là góc AIA’ = 30o
\(\begin{array}{l}AI = \dfrac{{AB\sqrt 3 }}{2} = \dfrac{{3a}}{2}\\A'A = AI.\tan 30^\circ = \dfrac{{a\sqrt 3 }}{2}\end{array}\)
Hình chóp M.BCC’B’ có diện tích đáy BCC’B’ là
\(S = BC.BB' = AB.A'A = \dfrac{{3{a^2}}}{2}\)
Vì MA // BB’ nên MA // (BCC’B’) nên chiều cao của hình chóp M.BCC’B’ bằng khoảng cách từ A đến mặt phẳng (BCC’B’) và bằng \(h = AI = \dfrac{{3a}}{2}\)
Thể tích hình chóp là \(V = \dfrac{1}{3}Sh = \dfrac{{3{a^3}}}{4}\)
Chọn đáp án A







