Câu hỏi
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là trung điểm SB và G là trọng tâm tam giác SBC. Gọi V, V’ lần lượt là thể tích của các khối chóp M. ABC và G.ABD, tính tỉ số \(\dfrac{V}{{V'}}\)
- A \(\dfrac{V}{{V'}} = \dfrac{3}{2}\)
- B \(\dfrac{V}{{V'}} = \dfrac{4}{3}\)
- C \(\dfrac{V}{{V'}} = \dfrac{5}{3}\)
- D \(\dfrac{V}{{V'}} = \dfrac{2}{3}\)
Phương pháp giải:
Tỉ lệ thể tích của hai khối chóp có cùng diện tích đáy bằng tỉ lệ 2 chiều cao của chúng
Lời giải chi tiết:
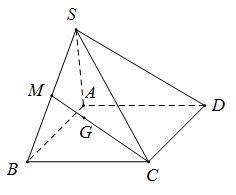
Hai khối chóp M.ABC và G.ABD có diện tích đáy bằng nhau nên tỉ lệ thể tích của chúng bằng tỉ lệ 2 chiều cao.
Vì MG cắt mặt phẳng đáy tại C nên tỉ lệ 2 chiều cao của 2 khối chóp là
\(\dfrac{{MC}}{{GC}} = \dfrac{3}{2} \Rightarrow \dfrac{V}{{V'}} = \dfrac{3}{2}\)
Chọn đáp án A
Câu hỏi trước
