Câu hỏi
Cho hình lăng trụ tam giác \(ABC.A’B’C’\). Gọi \(M,\, N\) lần lượt là trung điểm của \(BB’,\, CC’\). Mặt phẳng \((A’MN)\) chia khối lăng trụ thành hai phần, \({{V}_{1}}\) là thể tích của phần đa diện chứa điểm \(B\), \({{V}_{2}}\) là phần đa diện còn lại. Tính tỉ số \(\dfrac{{{V}_{1}}}{{{V}_{2}}}.\)
- A \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=\frac{7}{2}\)
- B \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=2\)
- C \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=3\)
- D \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=\frac{5}{2}\)
Phương pháp giải:
Sử dụng công thức tính thể tích của khối chóp và tỉ lệ thể tích để làm bài toán.
Lời giải chi tiết:
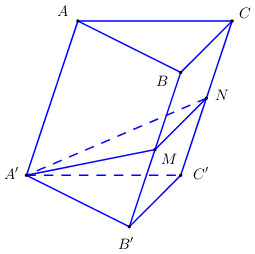
Vì \(M,\,\,N\) lần lượt là trung điểm của \(B{B}',\,\,\,C{C}'.\)
Suy ra \({{S}_{MN{C}'{B}'}}=\dfrac{1}{2}{{S}_{A'.BC{C}'{B}'}}\Rightarrow {{V}_{{A}'.MN{C}'{B}'}}=\dfrac{1}{2}{{V}_{BC{C}'{B}'}}=\dfrac{1}{2}\left( {{V}_{ABC.{A}'{B}'{C}'}}-{{V}_{{A}'.ABC}} \right)\)
Mà \({{V}_{{A}'.ABC}}=\dfrac{1}{3}{{V}_{ABC.{A}'{B}'{C}'}}\Rightarrow {{V}_{{A}'.MN{C}'{B}'}}=\dfrac{1}{2}\left( {{V}_{ABC.{A}'{B}'{C}'}}-\dfrac{1}{3}{{V}_{ABC.{A}'{B}'{C}'}} \right)=\dfrac{1}{3}{{V}_{ABC.{A}'{B}'{C}'}}.\)
Vậy tỉ số \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{{{V}_{{A}'MN.ABC}}}{{{V}_{{A}'.MN{C}'{B}'}}}=\dfrac{{{V}_{ABC.{A}'{B}'{C}'}}-\dfrac{1}{3}{{V}_{ABC.{A}'{B}'{C}'}}}{\dfrac{1}{3}{{V}_{ABC.{A}'{B}'{C}'}}}=2.\)
Chọn B.







