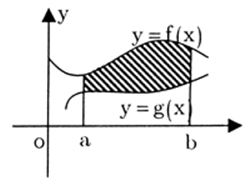
Câu hỏi
Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành.
Thể tích khối tròn xoay tạo thành được tính theo công thức nào ?
- A \(V=\int\limits_{a}^{b}{{{\left[ f\left( x \right)-g\left( x \right) \right]}^{\,2}}\text{d}x}.\)
- B \(V=\pi .\int\limits_{a}^{b}{\left| {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right|\text{d}x}.\)
- C \(V=\pi .\int\limits_{a}^{b}{{{\left[ f\left( x \right)-g\left( x \right] \right)}^{\,2}}\text{d}x}.\)
- D \(V=\pi .\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|\text{d}x}.\)
Phương pháp giải:
Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),y=g\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{\left| {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right|\text{d}x}.\)
Lời giải chi tiết:
Thể tích khối tròn xoay được tính theo công thức \(V=\pi .\int\limits_{a}^{b}{\left( {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right)\text{d}x}.\)
Chọn B.