Câu hỏi
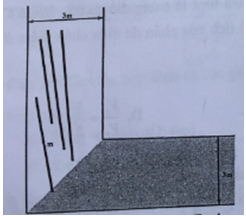
Một kênh dẫn nước theo vuông góc có bề rộng 3,0 m như hình vẽ. Cho 4 cây luồng (thẳng) có độ dài là 6,2m ; 8,3m ; 8,4m ; 9,0m trôi tự do trên kênh. Hỏi số cây luồng có thể trôi tự do qua góc kênh là bao nhiêu ?
- A 1
- B 4
- C 3
- D 2
Phương pháp giải:
Phương pháp :
Phân tích đề bài và tìm giá trị lớn nhất của cây luồng để có thể trôi qua khúc sông.
Lời giải chi tiết:
Cách giải:
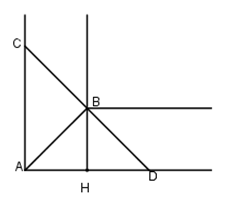
Xét tam giác vuông ABH ta dễ dàng tính được \(AB=3\sqrt{2}\).Để cây luồng có thể trôi qua khúc sông thì độ dài cây luồng không được vượt quá độ dài đoạn thẳng CD với CD là đoạn thẳng đi qua B và vuông góc với AB như hình vẽ.
Tam giác ACD vuông tại A và có AB là phân giác đồng thời là đường cao nên \(\Delta ACD\) cân tại B
\(\Rightarrow AB\) là trung tuyến ứng với cạnh huyền.
\(\Rightarrow AB=\frac{1}{2}CD\Rightarrow CD=2AB=6\sqrt{2}\approx 8,48\)
Vậy trong 4 cây luồng trên chỉ có cây luồng dài 9m không trôi qua được khúc sông.
Chọn C