Câu hỏi
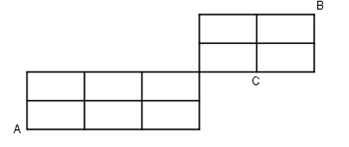
Một con thỏ di chuyển từ địa điểm A đến địa điểm B bằng cách qua các điểm nút (trong lưới cho ở hình vẽ) thì chỉ di chuyển sang phải hoặc đi lên (mỗi cách di chuyển như vậy xem là 1 cách đi). Biết nếu thỏ di chuyển đến nút C thì bị cáo ăn thịt, tính xác suất để thỏ đến được vị trí B.
- A \(\frac{1}{2}\)
- B \(\frac{2}{3}\)
- C \(\frac{3}{4}\)
- D \(\frac{5}{12}\)
Phương pháp giải:
Phương pháp :
Chia đường đi của thỏ thành 2 giai đoạn, tính số phần tử của không gian mẫu và số phần tử của biến cố A « thỏ đến được vị trí B » .
Lời giải chi tiết:
Cách giải :
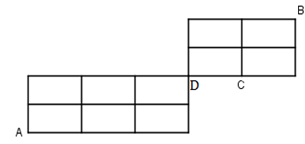
Từ A đến B nhất định phải đi qua D, ta chia làm 2 giai đoạn \(A\to D\) và \(D\to B\)
Từ \(A\to D\) có 9 cách.
Từ \(D\to B\) có 6 cách tính cả đi qua C và có 3 cách không đi qua C.
Không gian mẫu \({{n}_{\Omega }}=9.6=54\)
Gọi A là biến cố « thỏ đến được vị trí B » thì \({{n}_{A}}=9.3=27\)
Vậy \(P\left( A \right)=\frac{{{n}_{A}}}{{{n}_{\Omega }}}=\frac{27}{54}=\frac{1}{2}\)
Chọn A.