Câu hỏi
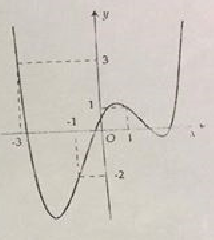
Hàm số \(y=f(x)\)có đồ thị \(y=f'(x)\) như hình vẽ.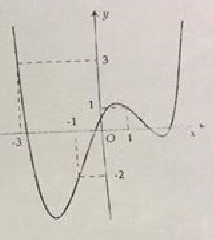
Xét hàm số \(g(x)=f(x)-\frac{1}{3}{{x}^{3}}-\frac{3}{4}{{x}^{2}}+\frac{3}{2}x+2017\)
Trong các mệnh đề dưới đây:
(I) \(g(0)<g(1).\)
(II) \(\underset{x\in \left[ -3;1 \right]}{\mathop{\min }}\,g(x)=g(-1).\)
(III) Hàm số \(g(x)\) nghịch biến trên (-3; -1).
(IV) \(\underset{x\in \left[ -3;1 \right]}{\mathop{\max }}\,g(x)=\underset{x\in \left[ -3;1 \right]}{\mathop{\max }}\,\left\{ g(-3);g(1) \right\}\).
Số mệnh đề đúng là:
- A 4
- B 3
- C 2
- D 1
Lời giải chi tiết:
Ta có \(g'(x)=f'(x)-{{x}^{2}}-\frac{3}{2}x+\frac{3}{2}=f'(x)-\left( {{x}^{2}}+\frac{3}{2}x-\frac{3}{2} \right)\)
Theo đồ thị, ta có: \(\left\{ \begin{array}{l}f'\left( { - 1} \right) = - 2\\f'\left( 1 \right) = 1\\f'\left( { - 3} \right) = 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}g'\left( { - 1} \right) = 0\\g'\left( 1 \right) = 0\\g'\left( { - 3} \right) = 0\end{array} \right.\)
Vẽ Parabol (P): \(y={{x}^{2}}+\frac{3}{2}x-\frac{3}{2}\) trên cùng hệ trục tọa độ của hàm số \(y=f'(x)\)
Ta có: Trên \((-3;-1)\) thì \(f'(x)<{{x}^{2}}+\frac{3}{2}x-\frac{3}{2}\Rightarrow g'(x)<0,\,\forall x\in (-3;-1)\)
Trên \((-1;1)\) thì \(f'(x)>{{x}^{2}}+\frac{3}{2}x-\frac{3}{2}\Rightarrow g'(x)>0,\,\forall x\in (-1;1)\)
Khi đó, ta có bảng biến thiên của hàm số \(g(x)\) trên đoạn \(\left[ -3;1 \right]\) như sau:
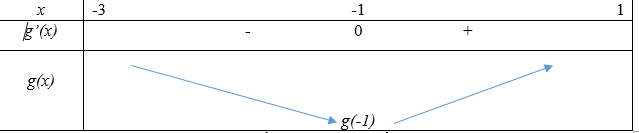
Vậy \(\underset{x\in \left[ -3;1 \right]}{\mathop{\min }}\,g(x)=g(-1),\,\,g(0)<g(1),\)hàm số \(g(x)\) nghịch biến trên \((-3;-1)\) và \(\underset{x\in \left[ -3;1 \right]}{\mathop{\max }}\,g(x)=\max \left\{ g(-3),g(1) \right\}\)
Chọn A.







