Phương pháp giải:

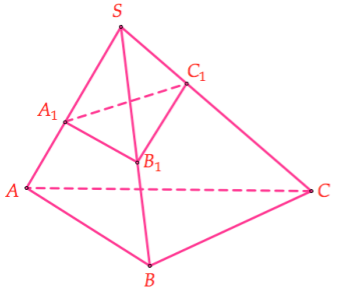
Sử dụng công thức tỉ số thể tích cho khối chóp tam giác

(Công thức Simson): Cho khối chóp S.ABC, các điểm \({{A}_{1}},\,{{B}_{1}},\,{{C}_{1}}\) lần lượt thuộc \(SA,\,SB,\,SC\). Khi đó,

\(\frac{{{V}_{S.\,{{A}_{1}}{{B}_{1}}{{C}_{1}}}}}{{{V}_{S.ABC}}}=\frac{S{{A}_{1}}}{SA}.\frac{S{{B}_{1}}}{SB}.\frac{S{{C}_{1}}}{SC}\)

Lời giải chi tiết:

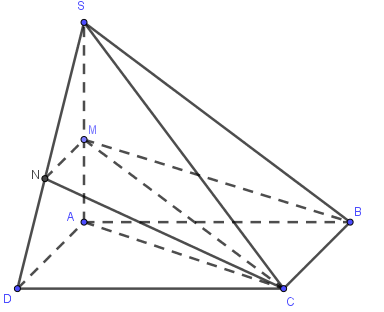
Giả sử (MBC) cắt SD tại N. Khi đó MN // BC // AD, suy ra \(\frac{SM}{SA}=\frac{SN}{SD}=k\,(k>0)\)

Ta có:  \(\frac{{{V}_{S.MBC}}}{{{V}_{S.ABC}}}=\frac{SM}{SA}=k,\,\,\frac{{{V}_{S.MNC}}}{{{V}_{S.ADC}}}=\frac{SM}{SA}.\frac{SN}{SD}={{k}^{2}}\)

Do đó: \(\frac{{{V}_{S.MBC}}}{{{V}_{S.ABCD}}}=\frac{k}{2};\,\,\,\frac{{{V}_{S.MNC}}}{{{V}_{S.ABCD}}}=\frac{{{k}^{2}}}{2}\)

Bài toán thỏa mãn khi  \(\frac{k}{2}+\frac{{{k}^{2}}}{2}=\frac{1}{2}\Leftrightarrow {{k}^{2}}+k-1=0\Rightarrow k=\frac{-1+\sqrt{5}}{2}\)

Chọn C.