Câu hỏi
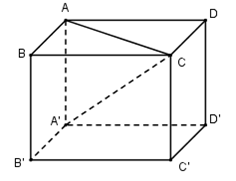
Tính thể tích V của khối lăng trụ tứ giác đều ABCD.A’B’C’D’ biết độ dài cạnh đáy bằng 2 đồng thời góc tạo bởi A’C và đáy (ABCD) bằng \({{30}^{0}}\)?
- A \(V=\frac{8\sqrt{6}}{3}\)
- B \(V=24\sqrt{6}\)
- C \(V=8\sqrt{6}\)
- D \(V=\frac{8\sqrt{6}}{9}\)
Phương pháp giải:
Phương pháp:
Lăng trụ tứ giác đều là lăng trụ đứng có đáy là hình vuông.
Xác định góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Áp dụng công thức tính thể tích khối lăng trụ \(V=Bh\) trong đó h là chiều cao và B là diện tích đáy lăng trụ.
Lời giải chi tiết:
Cách giải:
ABCD là hình vuông cạnh 2 nên \(AC=2\sqrt{2}\)Ta có: A là hình chiếu của A’ trên (ABCD) nên \(\left( A'C;\left( ABCD \right) \right)=\left( A'C;AC \right)=\widehat{A'CA}={{30}^{0}}\).
Xét tam giác vuông A’CA có \(A'A=AC.\tan 30=2\sqrt{2}.\frac{\sqrt{3}}{3}=\frac{2\sqrt{6}}{3}\)
Vậy \({{V}_{ABCD.A'B'C'D'}}=A'A.{{S}_{ABCD}}=\frac{2\sqrt{6}}{3}.4=\frac{8\sqrt{6}}{3}.\)
Chọn A.