Phương pháp giải:

- Gọi E là trung điểm của AB, vì \(\Delta SAB\) đều nên \(SE\bot AB\)

Mà  \(\left\{ \begin{array}{l}(SAB) \bot (ABCD)\\(SAB) \cap (ABCD) = AB\end{array} \right.\)  \(\Rightarrow SE\bot (ABCD)\).

- Xác định góc giữa mặt phẳng (SCD) với mặt phẳng (ABCD), biết rằng \(\left( SCD \right)\cap \left( ABCD \right)=CD,\,\,\left( SGE \right)\bot CD\)

( G là trung điểm của CD)  \(\Rightarrow \left( \widehat{(SCD),(ABCD)} \right)=\widehat{SGE}={{30}^{0}}\).

- Sử dụng công thức tính thể tích khối chóp: \(V=\frac{1}{3}S.h\), với S là diện tích đáy, h là chiều cao của khối chóp.

Lời giải chi tiết:

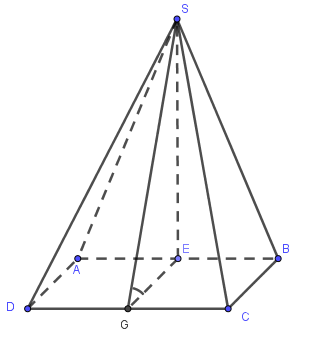
Gọi E là trung điểm của AB, \(SE=\frac{a\sqrt{3}}{2},\,SE\bot (ABCD)\)

Gọi G là trung điểm của CD. Khi đó: \(\left( \widehat{(SCD),(ABCD)} \right)=\widehat{SGE}={{30}^{0}}\)

\(EG=SE.\cot {{30}^{0}}=\frac{a\sqrt{3}}{2}.\sqrt{3}=\frac{3a}{2}\Rightarrow AD=BC=\frac{3a}{2}\)

\(\begin{array}{l} \Rightarrow {S_{ABCD}} = AB.CD = a.\frac{{3a}}{2} = \frac{{3{a^2}}}{2}\\ \Rightarrow V = \frac{1}{3}SE.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{2}.\frac{{3{a^2}}}{2} = \frac{{{a^3}\sqrt 3 }}{4}.\end{array}\)

Chọn B.