Phương pháp giải:

- Sử dụng lí thuyết: Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của 2 mặt phẳng đó vuông góc với mặt phẳng thứ ba.

- Tính độ dài đường cao SA dựa vào định lý Pi-ta-go.

- Sử dụng công thức tính thể tích khối chóp: \(V=\frac{1}{3}S.h\)

Lời giải chi tiết:

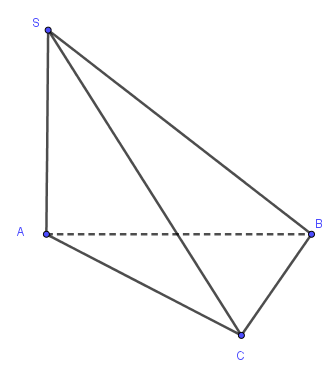
\(\left\{ \begin{array}{l}(SAB) \bot \left( {ABC} \right)\\(SAC) \bot \left( {ABC} \right)\\(SAB) \cap \left( {SAC} \right) = SA\end{array} \right. \Rightarrow SA \bot \left( {ABC} \right)\)

Tam giác SAC vuông tại A  Áp dụng định lý Pi-ta-go ta có:

\(\begin{array}{l}S{A^2} = S{C^2} - A{C^2} = {\left( {a\sqrt 3 } \right)^2} - {a^2} = 2{a^2}\\ \Rightarrow SA = a\sqrt 2 \end{array}\)

Tam giác ABC đều có cạnh bằng a  \(\Rightarrow {{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}\)

Thể tích khối chóp S.ABC: \(V=\frac{1}{3}S.h=\frac{1}{3}{{S}_{ABC}}.SA=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{3}}{4}.a\sqrt{2}=\frac{{{a}^{3}}\sqrt{6}}{12}\)

Chọn B.