Phương pháp giải:

- Xác định góc giữa SB và đáy là \(\widehat{SBA}\).

- Tính độ dài cạnh AB, BC của tam giác vuông cân ABC.

- Tính chiều cao SA của chóp:

\(SA=AB.\tan \widehat{SBA}=AB.\tan {{60}^{0}}\) .

- Sử dụng công thức tính thể tích khối chóp: \(V=\frac{1}{3}S.h\).

Với:     S là diện tích của đáy,

            h là chiều cao của khối chóp.

Lời giải chi tiết:

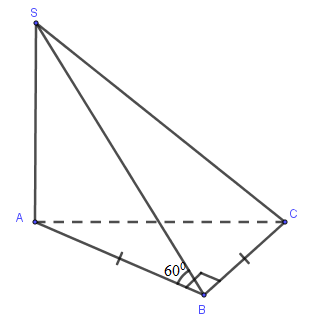
Vì SA vuông góc với (ABC) \(\Rightarrow \) A là hình chiếu của S trên (ABC) \(\Rightarrow \)AB là hình chiếu của SB trên (ABC)

\(\Rightarrow (SB,(ABC))=(SB,AB)=\widehat{SBA}={{60}^{0}}\)

Tam giác vuông cân ABC tại B \(\Rightarrow \)\(AB=BC=AC.\sin {{45}^{0}}=AC.\frac{\sqrt{2}}{2}=\frac{a\sqrt{2}}{2}\)

Tam giác SAB vuông tại A \(\Rightarrow \)\(SA=AB.\tan \widehat{SBA}=\frac{a\sqrt{2}}{2}.\tan {{60}^{0}}=\frac{a\sqrt{6}}{2}\)

Thể tích khối chóp S.ABC là: \(V=\frac{1}{3}{{S}_{ABC}}.SA=\frac{1}{3}.\left( \frac{1}{2}.\frac{a\sqrt{2}}{2}.\frac{a\sqrt{2}}{2} \right).\frac{a\sqrt{6}}{2}=\frac{{{a}^{3}}\sqrt{6}}{24}\).

Chọn A.