Câu hỏi
Cho hình chóp S.ABC. Gọi \(A',B’\) lần lượt là trung điểm cạnh SA, SB. Gọi \({{V}_{1}},{{V}_{2}}\) lần lượt là thể tích của khối chóp \(S.A'B'C\) và \(S.ABC.\) Tỉ số \(\dfrac{{{V}_{1}}}{{{V}_{2}}}\) bằng:
- A \(\frac{1}{2}\)
- B \(\frac{1}{3}\)
- C \(\frac{1}{4}\)
- D \(\frac{1}{8}\)
Phương pháp giải:
Sử dụng công thức tính tỉ lệ thể tích trong khối chóp tam giác: \(\frac{{{V}_{S.A'B'C'}}}{{{V}_{S.ABC}}}=\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC}\)
Lời giải chi tiết:
Ta có: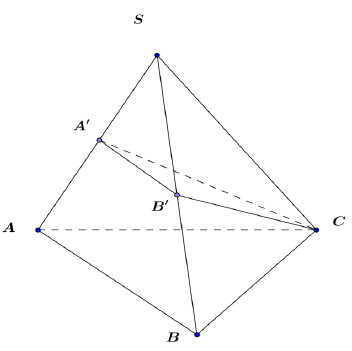
\(\frac{{{V}_{S.A'B'C}}}{{{V}_{S.ABC}}}=\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC}{SC}=\frac{1}{2}.\frac{1}{2}.1=\frac{1}{4}\)
Đáp án C
Câu hỏi trước
