Câu hỏi
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật \(AD=2a,AB=a.\) Gọi H là trung điểm cạnh AD, biết \(SH\bot (ABCD),SA=a\sqrt{5}.\) Thể tích khối chóp S.ABCD tính theo a là:.
- A \(\frac{2{{a}^{3}}\sqrt{3}}{3}\)
- B \(\frac{4{{a}^{3}}\sqrt{3}}{3}\)
- C \(\frac{4{{a}^{3}}}{3}\)
- D \(\frac{2{{a}^{3}}}{3}\)
Phương pháp giải:
Thể tích khối chóp \(V=\frac{1}{3}Sh\)
Lời giải chi tiết:
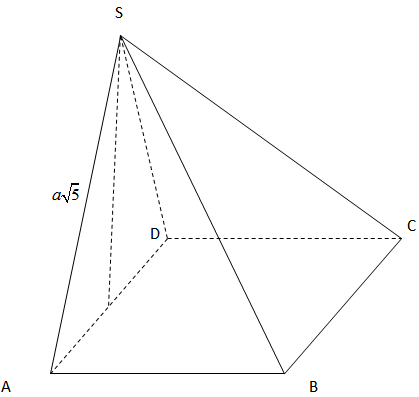
Gọi H là chân đường cao kẻ từ S đến (ABCD)
Ta có \({{S}_{ABCD}}=2{{a}^{2}}\)
\(SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=2a\)
\(\Rightarrow {{V}_{S.ABCD}}=\frac{1}{3}2{{a}^{2}}2a=\frac{4}{3}{{a}^{3}}.\)
Đáp án C
Câu hỏi trước
