Phương pháp giải:

- Xác định tọa độ 2 điểm cực trị A, B.

- Tính diện tích tam giác OAB theo công thức: \(S=\frac{1}{2}a.h\) (với a là độ dài đáy, h là độ dài đường cao tương ứng với đáy đã chọn).

Lời giải chi tiết:

\(\begin{array}{l}y = {x^3} - 3x + 2 \Rightarrow y' = 3{x^2} - 3\\y' = 0 \Leftrightarrow x =  \pm 1\end{array}\)

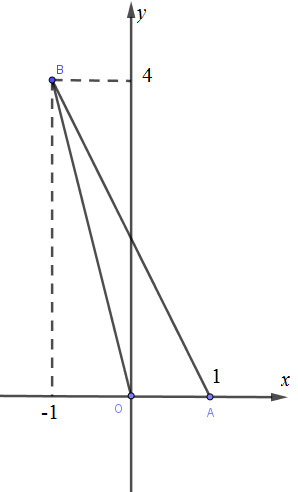
Tọa độ 2 điểm cực trị : \(A(1;\,0),\,\,B(-1;4)\)

Cách 1:

\({{S}_{\Delta OAB}}=\frac{1}{2}.OA.{{d}_{(B,OA)}}=\frac{1}{2}.\left| {{x}_{A}} \right|.\left| {{y}_{B}} \right|=\frac{1}{2}.\left| 1 \right|.\left| 4 \right|=2\)

Cách 2:

Tính \(AB=\sqrt{{{(-1-1)}^{2}}+{{(4-0)}^{2}}}=2\sqrt{5}\)

Lập phương trình đường thẳng AB:  \(2x+y-2=0\)

=> \(d(O,AB)=\frac{\left| 2.0+0-2 \right|}{\sqrt{{{2}^{2}}+1}}=\frac{2}{\sqrt{5}}\)

\({{S}_{\Delta OAB}}=\frac{1}{2}.AB.d(O;AB)=\frac{1}{2}.2\sqrt{5}.\frac{2}{\sqrt{5}}=2.\)

Chọn A.