Câu hỏi
Cho hình chóp S.ABC có \(SA\bot \left( ABC \right),\) tam giác ABC vuông tại B, \(AB=a,AC=a\sqrt{3},SB=a\sqrt{5}.\) Thể tích khối chóp S.ABC tính theo a là:
- A \(\frac{{{a}^{3}}\sqrt{2}}{3}\)
- B \(\frac{{{a}^{3}}\sqrt{6}}{4}\)
- C \(\frac{{{a}^{3}}\sqrt{6}}{6}\)
- D \(\frac{{{a}^{3}}\sqrt{15}}{6}\)
Phương pháp giải:
Thể tích khối chóp \(V=\frac{1}{3}Sh\)(Sử dụng định lý Py-ta-go để tính các cạnh \(SA,BC\))
Lời giải chi tiết:
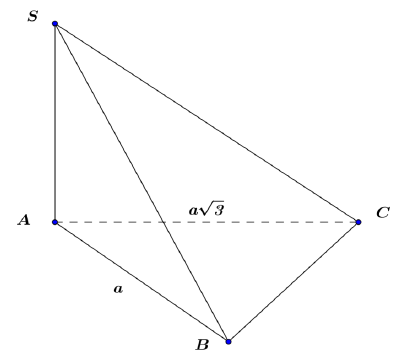
Dễ có \(BC=a\sqrt{2},SA=2a\)
\(\Rightarrow {{V}_{S.ABC}}=\frac{1}{3}\left( \frac{1}{2}AB.BC \right).SA=\frac{{{a}^{3}}\sqrt{2}}{3}.\)
Đáp án A
Câu hỏi trước
