Phương pháp giải:

Xác định góc giữa đường thẳng \(SC\)và mặt phẳng đáy theo định nghĩa: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.

Thể tích khối chóp \(V=\frac{1}{3}Sh\).

Lời giải chi tiết:

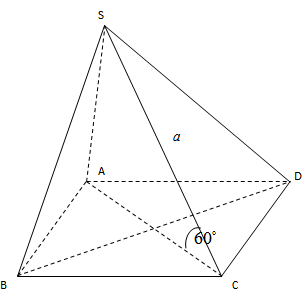
Vì A là hình chiếu của \(S\) lên \(\left( ABCD \right)\) nên\(\widehat{\left( SC,\left( ABCD \right) \right)}=\widehat{\left( SC,AC \right)}=\widehat{SCA}={{60}^{0}}\)

Ta có \(AC=SC\cos {{60}^{\circ }}=\frac{a}{2}.\)

\(SA=SC.\sin {{60}^{\circ }}=\frac{a\sqrt{3}}{2}\)

\(AB=BC=CD=DA=AC.\sin {{45}^{0}}=\frac{a}{2}\sin {{45}^{0}}=\frac{\sqrt{2}}{4}a\)

\(\Rightarrow {{S}_{ABCD}}=\frac{\sqrt{2}}{4}a\frac{\sqrt{2}}{4}a=\frac{{{a}^{2}}}{8}\)

\(\Rightarrow {{V}_{S.ABCD}}=\frac{1}{3}.\frac{{{a}^{2}}}{8}.\frac{a\sqrt{3}}{2}=\frac{{{a}^{3}}\sqrt{3}}{48}.\)

Đáp án D