Câu hỏi
Cho hình chóp đều S.ABCD có chiều cao bằng 3a và cạnh đáy bằng 4a. Thể tích khối chóp đều S.ABCD tính theo a là:
- A \(48{{a}^{3}}\)
- B \(16{{a}^{2}}\)
- C \(48{{a}^{2}}\)
- D \(16{{a}^{3}}\)
Phương pháp giải:
Thể tích khối chóp \(V=\frac{1}{3}S.h\).
Lời giải chi tiết:
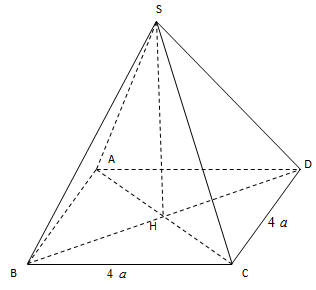
Ta có: \(V=\frac{1}{3}.{{S}_{ABCD}}.SH=\frac{1}{3}\left( 4a.4a \right).3a=16{{a}^{3}}\)
Đáp án D
Câu hỏi trước
